Chứng Minh Công Thức Tính Khoảng Cách Giữa 2 Điểm

Công thức tính khoảng cách giữa 2 điểm là một kiến thức toán học cơ bản, nhưng ứng dụng của nó lại vô cùng rộng rãi, từ việc đo đạc trong xây dựng đến định vị GPS. Bài viết này sẽ giúp bạn hiểu rõ cách chứng minh công thức, cũng như những ứng dụng thực tiễn của nó.

Công Thức Khoảng Cách Giữa Hai Điểm Trong Mặt Phẳng

Chúng ta sẽ bắt đầu với trường hợp đơn giản nhất: tính khoảng cách giữa hai điểm trên mặt phẳng. Giả sử ta có hai điểm A(x₁, y₁) và B(x₂, y₂). Khoảng cách giữa hai điểm này, ký hiệu là AB, được tính bằng công thức:

AB = √[(x₂ – x₁)² + (y₂ – y₁)²]

Công thức này được suy ra từ định lý Pythagore.

Hãy tưởng tượng ta vẽ một tam giác vuông với A và B là hai đỉnh, và đỉnh thứ ba là C(x₂, y₁). Độ dài cạnh AC chính là |x₂ – x₁|, và độ dài cạnh BC là |y₂ – y₁|. Áp dụng định lý Pythagore, ta có AB² = AC² + BC², hay AB = √[(x₂ – x₁)² + (y₂ – y₁)²].

Chứng Minh Công Thức Tính Khoảng Cách Giữa 2 Điểm Trong Không Gian

Trong không gian ba chiều, với hai điểm A(x₁, y₁, z₁) và B(x₂, y₂, z₂), công thức tính khoảng cách phức tạp hơn một chút nhưng vẫn dựa trên nguyên lý tương tự:

AB = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²]

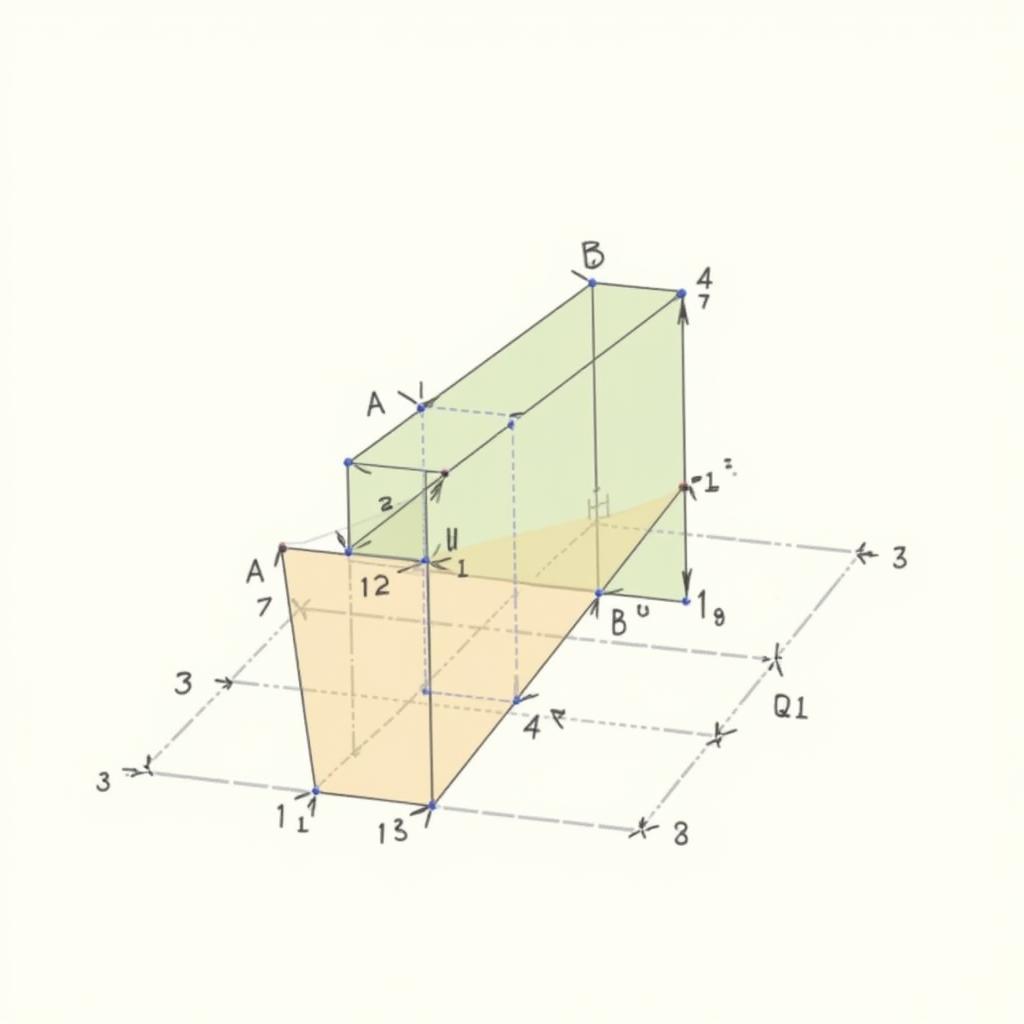Chứng minh khoảng cách giữa hai điểm trong không gian

Việc chứng minh cũng sử dụng định lý Pythagore, nhưng lần này ta áp dụng nó hai lần. Chi tiết chứng minh sẽ được trình bày trong phần sau.

Chi Tiết Chứng Minh Công Thức Khoảng Cách Trong Không Gian

Để chứng minh công thức khoảng cách trong không gian, ta hình dung một hình hộp chữ nhật với A và B là hai đỉnh đối diện. Đầu tiên, ta tính khoảng cách giữa hai điểm trên mặt phẳng xy, giả sử là điểm C(x₂, y₂, z₁). Khoảng cách AC được tính bằng √[(x₂ – x₁)² + (y₂ – y₁)²]. Sau đó, ta áp dụng định lý Pythagore cho tam giác vuông ABC, với AC là cạnh nằm trên mặt phẳng xy và BC là cạnh song song với trục z. Ta có BC = |z₂ – z₁|. Cuối cùng, ta có AB = √[AC² + BC²] = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²].

Ứng Dụng Của Công Thức Khoảng Cách

Công thức tính khoảng cách có rất nhiều ứng dụng trong thực tế:

Đo đạc trong xây dựng: Xác định khoảng cách giữa các điểm trên bản vẽ kỹ thuật.
Định vị GPS: Tính toán khoảng cách giữa các địa điểm trên bản đồ.
Thiết kế đồ họa: Tính toán khoảng cách giữa các đối tượng trong không gian ảo.
Phân tích dữ liệu: Đo lường sự tương đồng giữa các điểm dữ liệu.

Trả Lời Các Câu Hỏi:

What Chứng Minh Công Thức Tính Khoảng Cách Giữa 2 điểm? Bài viết này chứng minh công thức tính khoảng cách giữa hai điểm trong mặt phẳng và không gian bằng cách sử dụng định lý Pythagore.
Who sử dụng công thức tính khoảng cách giữa 2 điểm? Công thức này được sử dụng rộng rãi bởi các kỹ sư, nhà khoa học, nhà thiết kế đồ họa và nhiều ngành nghề khác.
When cần chứng minh công thức tính khoảng cách giữa 2 điểm? Việc chứng minh công thức này giúp hiểu rõ bản chất của nó và áp dụng đúng trong các bài toán phức tạp hơn.
Where áp dụng công thức tính khoảng cách giữa 2 điểm? Công thức này được áp dụng trong nhiều lĩnh vực, từ toán học đến vật lý, kỹ thuật, và khoa học máy tính.
Why cần công thức tính khoảng cách giữa 2 điểm? Công thức này là nền tảng cho nhiều phép tính hình học và có ứng dụng rộng rãi trong thực tế.
How chứng minh công thức tính khoảng cách giữa 2 điểm? Như đã trình bày ở trên, chứng minh dựa trên định lý Pythagore.

Kết luận

Công thức tính khoảng cách giữa 2 điểm là một công cụ toán học quan trọng với ứng dụng rộng rãi. Hiểu rõ cách chứng minh công thức này giúp bạn nắm vững kiến thức cơ bản và áp dụng nó một cách hiệu quả trong học tập và công việc.

FAQ

Câu hỏi 1: Định lý Pythagore là gì?
- Trả lời: Định lý Pythagore phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Câu hỏi 2: Làm thế nào để áp dụng công thức khoảng cách trong không gian nhiều chiều hơn?
- Trả lời: Công thức có thể được mở rộng cho không gian n chiều bằng cách thêm các thành phần bình phương của hiệu tọa độ tương ứng.
Câu hỏi 3: Có công cụ nào giúp tính toán khoảng cách giữa hai điểm tự động không?
- Trả lời: Có rất nhiều công cụ trực tuyến và phần mềm toán học có thể tính toán khoảng cách giữa hai điểm một cách nhanh chóng.
Câu hỏi 4: Khoảng cách giữa hai điểm có luôn là số dương không?
- Trả lời: Đúng, khoảng cách luôn là số dương hoặc bằng 0 nếu hai điểm trùng nhau.
Câu hỏi 5: Ngoài định lý Pythagore, còn cách nào khác để chứng minh công thức khoảng cách không?
- Trả lời: Có, có thể sử dụng vectơ để chứng minh công thức này.