Chứng Minh Công Thức Thể Tích Hình Chóp Cụt là một kiến thức quan trọng trong hình học không gian. Bài viết này sẽ hướng dẫn bạn chi tiết cách chứng minh công thức này, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và áp dụng hiệu quả. chứng minh công thức thể tích hình chóp
Khái Niệm Hình Chóp Cụt và Các Yếu Tố Liên Quan
Hình chóp cụt được tạo ra bằng cách cắt một hình chóp bởi một mặt phẳng song song với mặt đáy. Để hiểu rõ hơn về công thức thể tích, chúng ta cần nắm vững các yếu tố cấu thành hình chóp cụt: đáy lớn, đáy nhỏ, chiều cao và đường sinh. Đáy lớn và đáy nhỏ là hai đa giác đồng dạng. Chiều cao là khoảng cách giữa hai mặt đáy. Đường sinh là đoạn thẳng nối từ đỉnh của đáy nhỏ đến đỉnh tương ứng của đáy lớn.
Chứng Minh Công Thức Thể Tích Hình Chóp Cụt
Công thức thể tích hình chóp cụt được biểu diễn như sau: V = (1/3) h (S1 + S2 + √(S1*S2)), trong đó:
- V là thể tích hình chóp cụt.
- h là chiều cao của hình chóp cụt.
- S1 là diện tích đáy lớn.
- S2 là diện tích đáy nhỏ.
Để chứng minh công thức này, ta có thể sử dụng phương pháp bổ sung hình chóp. Bằng cách kéo dài các cạnh bên của hình chóp cụt, ta sẽ tạo ra một hình chóp hoàn chỉnh. chứng minh các công thức tính thể tích hình chóp Thể tích hình chóp cụt sẽ bằng thể tích hình chóp lớn trừ đi thể tích hình chóp nhỏ được tạo thành.
Chi Tiết Các Bước Chứng Minh
- Xác định thể tích hình chóp lớn: V_lớn = (1/3) H S1, với H là chiều cao của hình chóp lớn.
- Xác định thể tích hình chóp nhỏ: V_nhỏ = (1/3) (H – h) S2, với (H – h) là chiều cao của hình chóp nhỏ.
- Tính thể tích hình chóp cụt: V = V_lớn – V_nhỏ.
- Sử dụng tính chất đồng dạng của hai đáy và tỉ lệ giữa các chiều cao, ta có thể rút gọn biểu thức trên về dạng V = (1/3) h (S1 + S2 + √(S1*S2)).
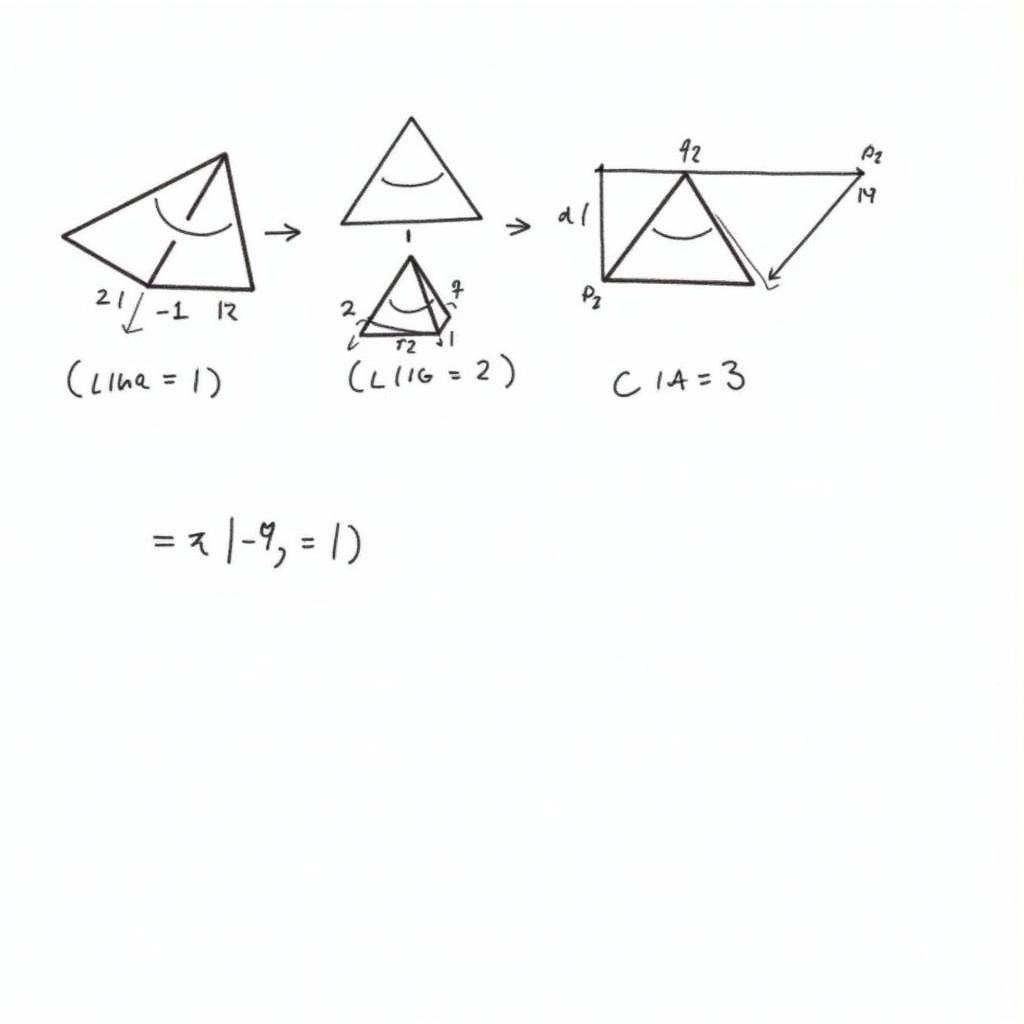 Chứng Minh Công Thức Thể Tích Hình Chóp Cụt
Chứng Minh Công Thức Thể Tích Hình Chóp Cụt
Trả Lời Các Câu Hỏi
- What chứng minh công thức thể tích hình chóp cụt? Chứng minh công thức thể tích hình chóp cụt liên quan đến việc sử dụng khái niệm bổ sung hình chóp và tính chất đồng dạng của hai đáy.
- Who cần chứng minh công thức thể tích hình chóp cụt? Học sinh, sinh viên, và những người làm việc trong lĩnh vực liên quan đến hình học không gian cần hiểu và biết cách chứng minh công thức này.
- When cần chứng minh công thức thể tích hình chóp cụt? Kiến thức này thường được học trong chương trình Toán THCS và THPT, và được áp dụng trong các bài toán liên quan.
- Where áp dụng chứng minh công thức thể tích hình chóp cụt? Công thức này được áp dụng trong nhiều lĩnh vực, từ tính toán thể tích các vật thể trong thực tế đến thiết kế kiến trúc và kỹ thuật.
- Why cần chứng minh công thức thể tích hình chóp cụt? Việc chứng minh giúp hiểu sâu hơn về công thức và cách áp dụng, đồng thời rèn luyện tư duy logic và khả năng giải quyết vấn đề.
- How chứng minh công thức thể tích hình chóp cụt? Phương pháp bổ sung hình chóp và tính chất đồng dạng là chìa khóa để chứng minh công thức này.
Bổ Sung Trích Dẫn Từ Chuyên Gia Giả Định
TS. Nguyễn Văn Toán, chuyên gia hình học tại Đại học Khoa học Tự nhiên Hà Nội, cho biết: “Việc nắm vững chứng minh công thức thể tích hình chóp cụt không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn phát triển tư duy hình học không gian, một kỹ năng quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật.”
 Áp Dụng Công Thức Thể Tích Hình Chóp Cụt
Áp Dụng Công Thức Thể Tích Hình Chóp Cụt
Ông cũng nhấn mạnh: “Hiểu rõ bản chất của chứng minh sẽ giúp học sinh nhớ lâu hơn và áp dụng linh hoạt hơn trong các tình huống thực tế.”
Kết luận
Chứng minh công thức thể tích hình chóp cụt là một phần quan trọng trong hình học không gian. Bài viết này đã cung cấp hướng dẫn chi tiết về cách chứng minh và áp dụng công thức. Hy vọng bài viết sẽ giúp bạn nắm vững kiến thức này và áp dụng thành công trong học tập và công việc. Hãy tiếp tục tìm hiểu và khám phá thêm những kiến thức thú vị khác trong hình học.
FAQ
- Nêu Câu Hỏi: Công thức thể tích hình chóp cụt là gì?
Trả Lời Chi tiết Câu Hỏi: V = (1/3) h (S1 + S2 + √(S1*S2)) - Nêu Câu Hỏi: h trong công thức là gì?
Trả Lời Chi tiết Câu Hỏi: h là chiều cao của hình chóp cụt. - Nêu Câu Hỏi: S1 và S2 trong công thức đại diện cho điều gì?
Trả Lời Chi tiết Câu Hỏi: S1 là diện tích đáy lớn, S2 là diện tích đáy nhỏ. - Nêu Câu Hỏi: Làm thế nào để tính chiều cao của hình chóp cụt?
Trả Lời Chi tiết Câu Hỏi: Chiều cao là khoảng cách giữa hai mặt đáy. Có thể tính bằng cách sử dụng định lý Pytago trong tam giác vuông được tạo bởi chiều cao, đường sinh và hiệu của bán kính/ cạnh đáy lớn và đáy nhỏ. - Nêu Câu Hỏi: Hình chóp cụt có thể có đáy là hình gì?
Trả Lời Chi tiết Câu Hỏi: Đáy của hình chóp cụt có thể là bất kỳ đa giác nào, miễn là hai đáy đồng dạng. - Nêu Câu Hỏi: Ứng dụng của công thức thể tích hình chóp cụt trong thực tế là gì?
Trả Lời Chi tiết Câu Hỏi: Công thức này được ứng dụng trong tính toán thể tích các vật thể trong xây dựng, kiến trúc, và nhiều lĩnh vực khác. - Nêu Câu Hỏi: Phương pháp nào được sử dụng để chứng minh công thức thể tích hình chóp cụt?
Trả Lời Chi tiết Câu Hỏi: Phương pháp bổ sung hình chóp. - Nêu Câu Hỏi: Tính chất nào của hai đáy hình chóp cụt được sử dụng trong chứng minh?
Trả Lời Chi tiết Câu Hỏi: Tính chất đồng dạng. - Nêu Câu Hỏi: Có cách nào khác để chứng minh công thức này không?
Trả Lời Chi tiết Câu Hỏi: Có thể sử dụng tích phân để chứng minh công thức này, tuy nhiên phương pháp bổ sung hình chóp thường được sử dụng do dễ hiểu hơn. - Nêu Câu Hỏi: Làm thế nào để phân biệt hình chóp cụt và hình chóp?
Trả Lời Chi tiết Câu Hỏi: Hình chóp cụt được tạo ra bằng cách cắt hình chóp bởi một mặt phẳng song song với đáy. Hình chóp có một đỉnh nhọn, trong khi hình chóp cụt có hai đáy là hai đa giác đồng dạng.