Giản đồ Frenet là công cụ mạnh mẽ trong hình học vi phân, giúp mô tả đường cong trong không gian ba chiều. Bài viết này sẽ chứng minh 2 công thức giản đồ Frenet quan trọng, giúp bạn hiểu rõ hơn về mối quan hệ giữa vectơ tiếp tuyến, vectơ pháp tuyến và vectơ nhị diện của một đường cong. Chúng ta sẽ cùng nhau khám phá chi tiết các khái niệm và ứng dụng của giản đồ Frenet, từ cơ bản đến nâng cao.

Khái niệm cơ bản về Giản đồ Frenet

Giản đồ Frenet được xây dựng dựa trên ba vectơ đơn vị: vectơ tiếp tuyến (T), vectơ pháp tuyến (N) và vectơ nhị diện (B). Ba vectơ này tạo thành một hệ quy chiếu trực chuẩn di động dọc theo đường cong, giúp ta phân tích các đặc trưng hình học của đường cong một cách hiệu quả. Vectơ tiếp tuyến (T) biểu thị hướng di chuyển của đường cong tại mỗi điểm. Vectơ pháp tuyến (N) chỉ hướng mà đường cong đang uốn cong. Cuối cùng, vectơ nhị diện (B) là tích có hướng của T và N, hoàn thiện hệ quy chiếu trực chuẩn.

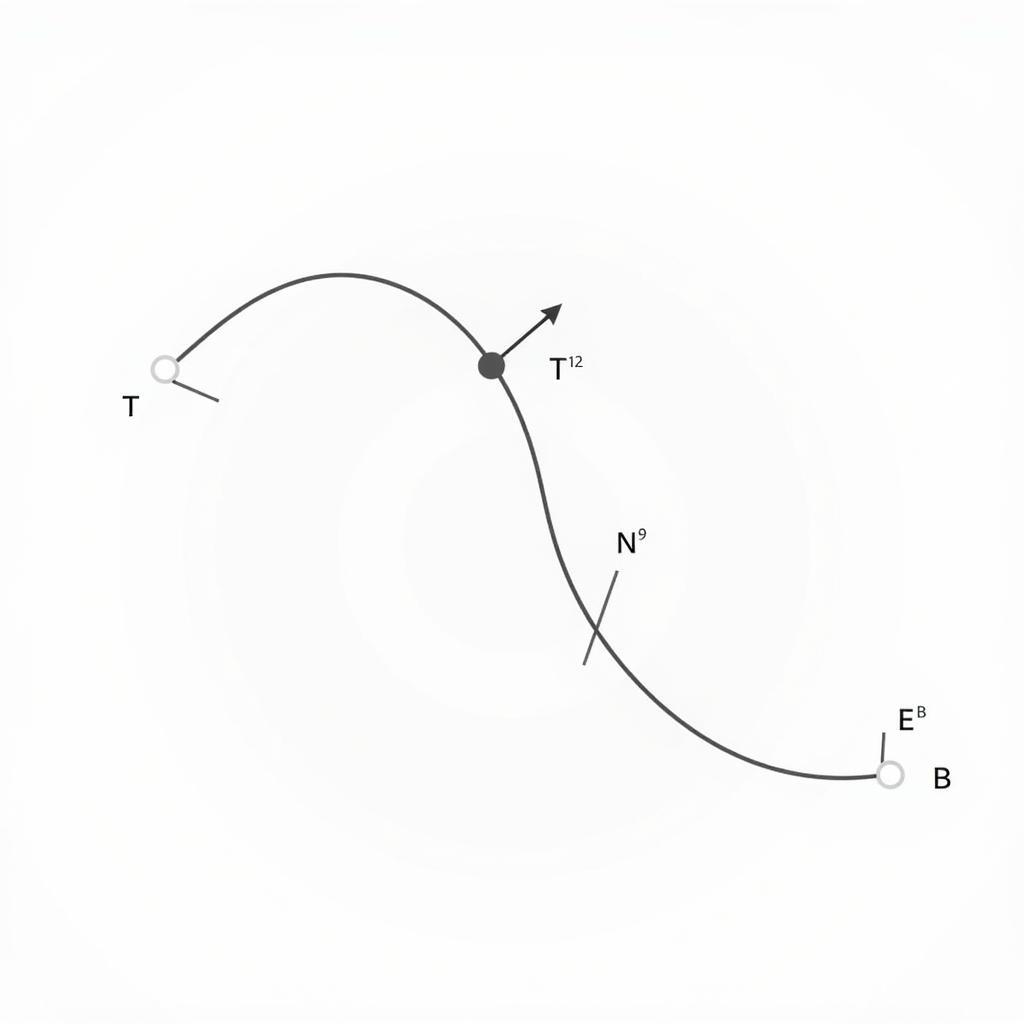Giản Đồ Frenet Cơ Bản

Công Thức Đạo Hàm của Vectơ Tiếp Tuyến (T)

Công thức đầu tiên chúng ta sẽ chứng minh là đạo hàm của vectơ tiếp tuyến (T) theo độ dài cung (s): dT/ds = κN, với κ là độ cong của đường cong. Độ cong κ thể hiện mức độ uốn cong của đường cong tại một điểm. Vectơ pháp tuyến (N) lại chỉ hướng của sự uốn cong đó. Vậy, công thức này cho thấy sự thay đổi của hướng di chuyển (dT/ds) tỉ lệ với độ cong (κ) và hướng uốn cong (N).

Chứng minh công thức dT/ds = κN

Ta biết rằng T là vectơ đơn vị, do đó T.T = 1. Đạo hàm hai vế theo s, ta có 2(dT/ds).T = 0, suy ra dT/ds vuông góc với T. Vì N là vectơ đơn vị cùng hướng với dT/ds, ta có thể viết dT/ds = κN, với κ là một hệ số tỉ lệ. κ chính là độ cong của đường cong.

Công Thức Đạo Hàm của Vectơ Nhị Diện (B)

Công thức thứ hai liên quan đến đạo hàm của vectơ nhị diện (B): dB/ds = -τN, với τ là độ xoắn của đường cong. Độ xoắn τ đo lường mức độ xoắn của đường cong ra khỏi mặt phẳng chứa T và N. Dấu trừ trong công thức cho thấy hướng thay đổi của B ngược với hướng của N.

Chứng minh công thức dB/ds = -τN

Ta có B = T x N. Đạo hàm hai vế theo s, ta được dB/ds = (dT/ds) x N + T x (dN/ds) = κN x N + T x (dN/ds) = T x (dN/ds). Do đó, dB/ds vuông góc với T. Mặt khác, B.B = 1, nên đạo hàm hai vế theo s ta có 2(dB/ds).B = 0, vậy dB/ds vuông góc với B. Vì dB/ds vuông góc với cả T và B, nó phải song song với N. Do đó, ta có thể viết dB/ds = -τN, với τ là độ xoắn.

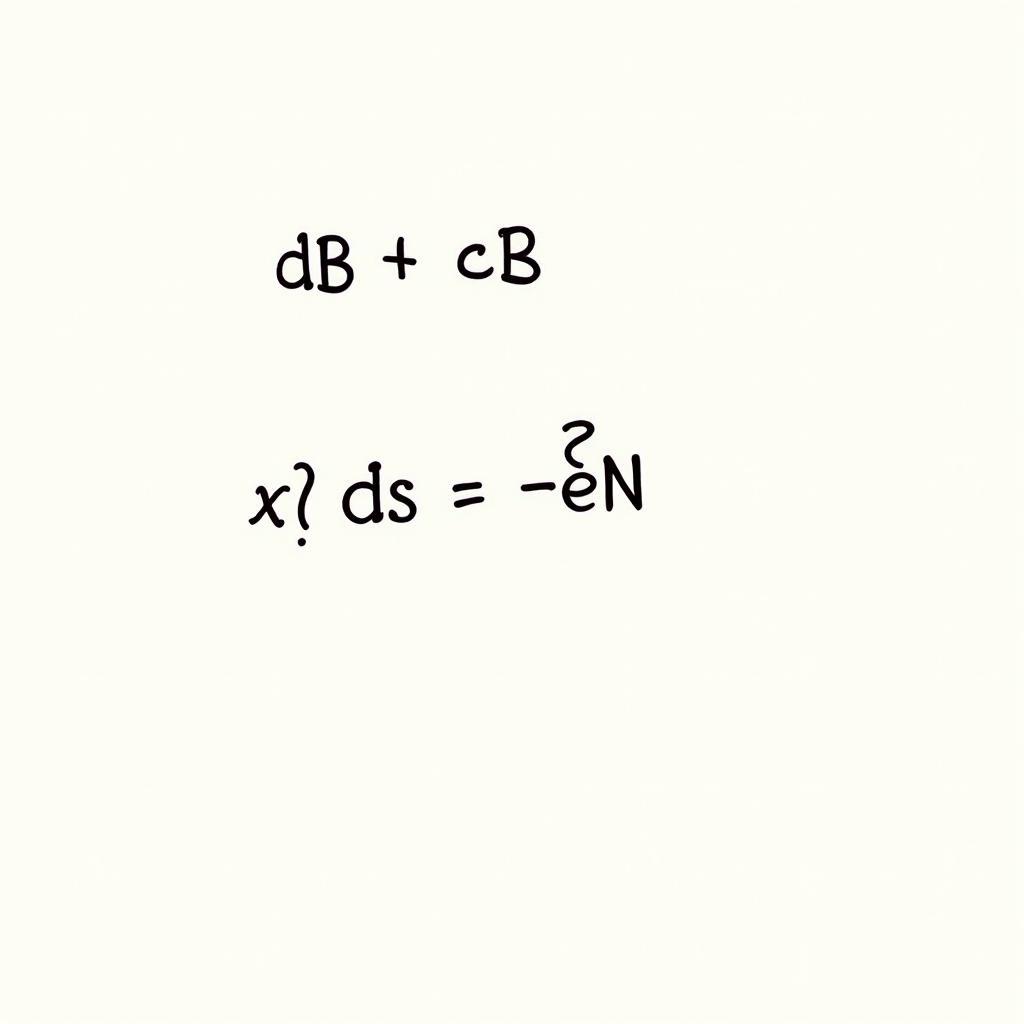Chứng Minh Công Thức Đạo Hàm B

Kết luận

Bài viết đã chứng minh 2 công thức giản đồ Frenet quan trọng: dT/ds = κN và dB/ds = -τN. Việc hiểu rõ các công thức này là nền tảng để phân tích các đặc trưng hình học của đường cong trong không gian ba chiều. Chứng minh 2 công thức giản đồ Frenet giúp chúng ta hiểu sâu hơn về mối quan hệ giữa độ cong, độ xoắn và các vectơ trong giản đồ Frenet.

FAQ

1. Giản đồ Frenet là gì?

Giản đồ Frenet là một hệ quy chiếu trực chuẩn di động dọc theo một đường cong trong không gian, bao gồm vectơ tiếp tuyến, vectơ pháp tuyến và vectơ nhị diện.

2. Độ cong và độ xoắn là gì?

Độ cong đo lường mức độ uốn cong của đường cong, còn độ xoắn đo lường mức độ xoắn của đường cong ra khỏi mặt phẳng.

3. Công thức Frenet-Serret là gì?

Công thức Frenet-Serret là tập hợp các công thức liên hệ giữa đạo hàm của các vectơ trong giản đồ Frenet với độ cong và độ xoắn.

4. Ứng dụng của giản đồ Frenet là gì?

Giản đồ Frenet được ứng dụng trong nhiều lĩnh vực như thiết kế đường bộ, đường sắt, đồ họa máy tính và robot.

5. Làm thế nào để tính toán độ cong và độ xoắn?

Độ cong và độ xoắn có thể được tính toán từ đạo hàm của vectơ vị trí của đường cong.

6. Vectơ tiếp tuyến, pháp tuyến và nhị diện có ý nghĩa gì?

Vectơ tiếp tuyến chỉ hướng di chuyển, vectơ pháp tuyến chỉ hướng uốn cong, và vectơ nhị diện hoàn thiện hệ quy chiếu trực chuẩn.

7. Tại sao cần phải hiểu về giản đồ Frenet?

Hiểu về giản đồ Frenet giúp ta phân tích và mô tả chính xác các đặc trưng hình học của đường cong.

8. Có những tài liệu nào để tìm hiểu thêm về giản đồ Frenet?

Bạn có thể tìm hiểu thêm về giản đồ Frenet trong các sách giáo khoa về hình học vi phân.

9. Giản đồ Frenet có liên quan gì đến hình học vi phân?

Giản đồ Frenet là một công cụ quan trọng trong hình học vi phân để nghiên cứu đường cong trong không gian.

10. Làm thế nào để áp dụng giản đồ Frenet trong thực tế?

Giản đồ Frenet có thể được áp dụng trong thiết kế đường cong, mô phỏng chuyển động và nhiều ứng dụng khác.