Công thức tính thể tích hình cầu, (4/3)πr³, là một kiến thức cơ bản trong hình học không gian. Bài viết này sẽ hướng dẫn bạn Cách Chứng Minh Công Thức Tính Thể Tích Hình Cầu một cách chi tiết và dễ hiểu, từ phương pháp tích phân đến các ví dụ minh họa thực tế.
Chứng Minh Công Thức Tính Thể Tích Hình Cầu Bằng Tích Phân
Phương pháp phổ biến nhất để chứng minh công thức tính thể tích hình cầu là sử dụng tích phân. Hãy tưởng tượng hình cầu được tạo thành từ vô số đĩa tròn mỏng xếp chồng lên nhau. Mỗi đĩa có bán kính thay đổi tùy thuộc vào vị trí của nó trên trục x.
Thiết Lập Hệ Tọa Độ và Phương Trình Đường Tròn
Đặt tâm hình cầu tại gốc tọa độ (0,0). Phương trình đường tròn trong mặt phẳng Oxy với bán kính r là x² + y² = r². Từ đây, ta có y = √(r² – x²).
Tính Diện Tích Đĩa Tròn
Diện tích của mỗi đĩa tròn mỏng là S = πy² = π(r² – x²).
Tích Phân để Tính Thể Tích
Để tính thể tích hình cầu, ta tích phân diện tích đĩa tròn theo biến x từ -r đến r:
V = ∫-rr π(r² – x²) dx = π [r²x – (x³/3)] -rr = (4/3)πr³
Vậy, ta đã chứng minh được công thức tính thể tích hình cầu là (4/3)πr³.
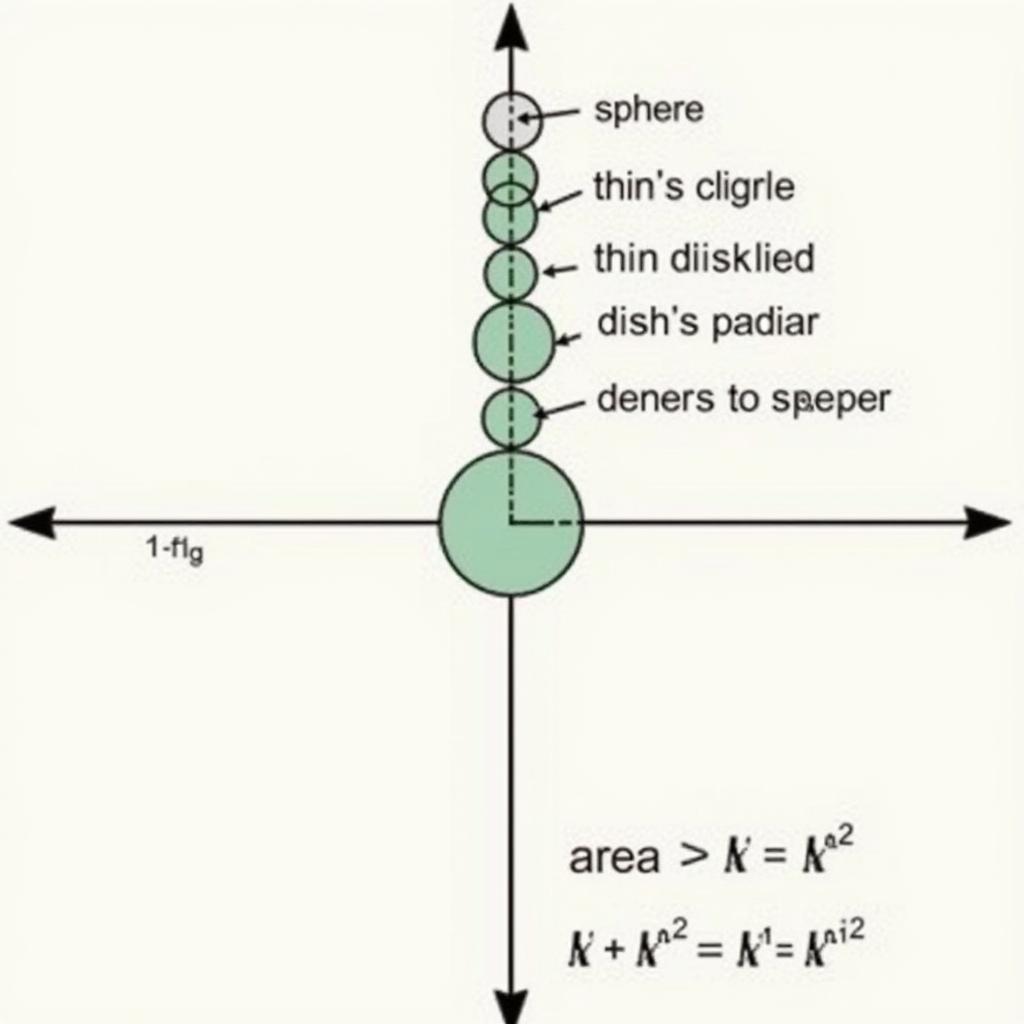Chứng minh công thức tính thể tích hình cầu bằng tích phân
Phương Pháp Khác: Nguyên Lý Cavalieri
Một cách tiếp cận khác để chứng minh công thức này là sử dụng Nguyên lý Cavalieri. Nguyên lý này so sánh thể tích của hai vật thể bằng cách so sánh diện tích của các mặt cắt ngang tương ứng.
So Sánh Hình Cầu và Hình Trụ Rỗng
Xét một hình cầu bán kính r nằm bên trong một hình trụ có bán kính đáy r và chiều cao 2r. Khoét bỏ hai hình nón có đỉnh tại tâm hình cầu và đáy trùng với đáy hình trụ. Phần còn lại của hình trụ (hình trụ rỗng) có cùng thể tích với hình cầu.
Áp Dụng Nguyên Lý Cavalieri
Theo Nguyên lý Cavalieri, nếu diện tích mặt cắt ngang của hai hình tại mọi vị trí đều bằng nhau, thì thể tích của chúng cũng bằng nhau. Diện tích mặt cắt ngang của hình trụ rỗng tại một vị trí bất kỳ cách tâm hình cầu một khoảng x là π(r² – x²), chính là diện tích mặt cắt ngang của hình cầu tại vị trí đó.
Tính Thể Tích Hình Trụ Rỗng
Thể tích hình trụ là πr²(2r) = 2πr³. Thể tích mỗi hình nón là (1/3)πr²r = (1/3)πr³. Vậy, thể tích hình trụ rỗng là 2πr³ – 2(1/3)πr³ = (4/3)πr³.
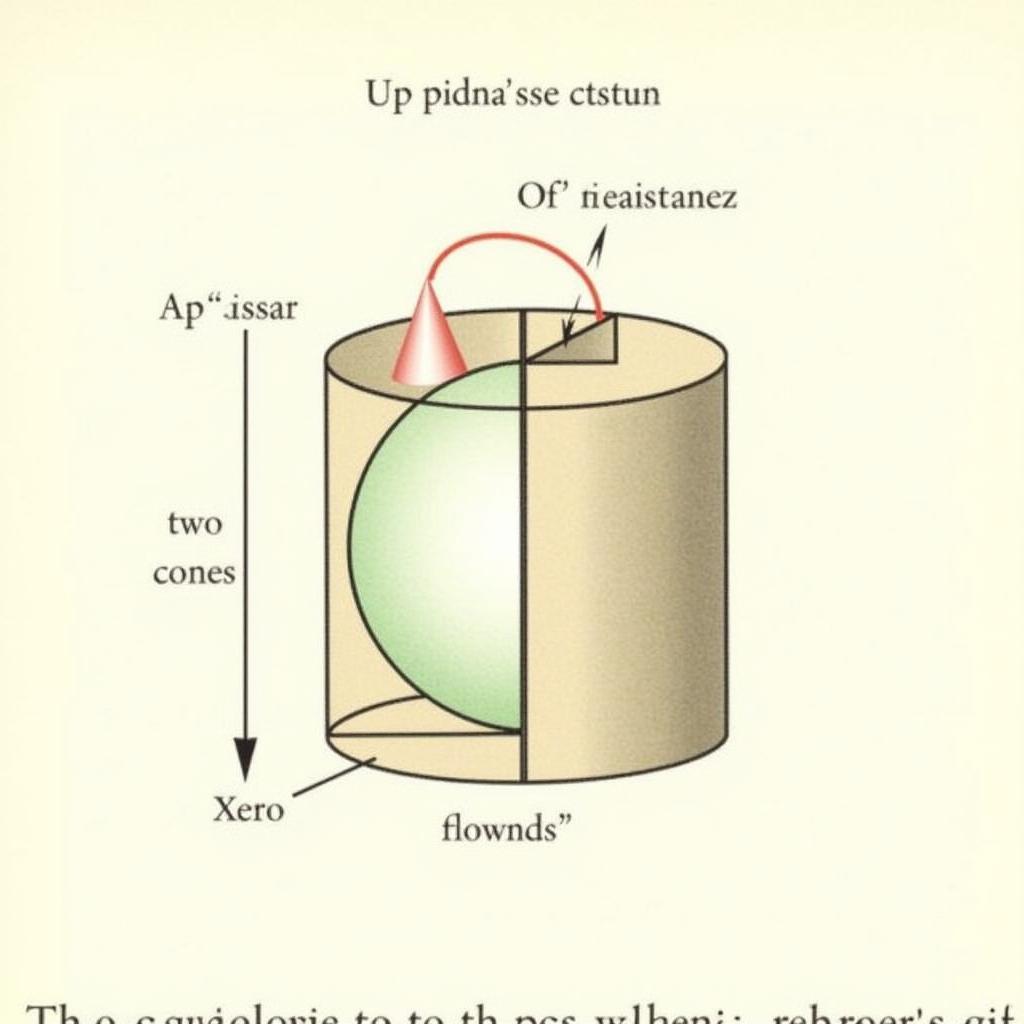Nguyên lý Cavalieri tính thể tích hình cầu
Trả Lời Các Câu Hỏi:
- What “cách chứng minh công thức tính thể tích hình cầu”? Cách chứng minh công thức tính thể tích hình cầu thường dùng tích phân hoặc Nguyên lý Cavalieri.
- Who “cách chứng minh công thức tính thể tích hình cầu”? Học sinh, sinh viên, và những người quan tâm đến toán học và hình học không gian thường tìm hiểu cách chứng minh này.
- When “cách chứng minh công thức tính thể tích hình cầu”? Kiến thức này thường được học ở bậc trung học phổ thông.
- Where “cách chứng minh công thức tính thể tích hình cầu”? Bạn có thể tìm thấy thông tin này trong sách giáo khoa, bài giảng toán học, và trên internet.
- Why “cách chứng minh công thức tính thể tích hình cầu”? Việc chứng minh công thức giúp hiểu sâu hơn về hình học không gian và bản chất của tích phân.
- How “cách chứng minh công thức tính thể tích hình cầu”? Bài viết này đã trình bày chi tiết hai phương pháp chứng minh.
Kết luận
Bài viết đã trình bày chi tiết cách chứng minh công thức tính thể tích hình cầu (4/3)πr³ bằng hai phương pháp: tích phân và Nguyên lý Cavalieri. Hiểu rõ cách chứng minh này không chỉ giúp bạn áp dụng công thức một cách chính xác mà còn nâng cao kiến thức về hình học không gian.
FAQ
-
Nêu Câu Hỏi: Ngoài tích phân và Nguyên lý Cavalieri, còn cách nào khác để chứng minh công thức thể tích hình cầu không?
Trả Lời Chi tiết Câu Hỏi: Có một số phương pháp khác, tuy nhiên phức tạp hơn và ít phổ biến hơn, ví dụ như sử dụng tọa độ cầu. -
Nêu Câu Hỏi: Ứng dụng của công thức tính thể tích hình cầu trong thực tế là gì?
Trả Lời Chi tiết Câu Hỏi: Công thức này được ứng dụng rộng rãi trong nhiều lĩnh vực, từ tính toán thể tích trái đất, thiết kế bể chứa, đến sản xuất bóng bay. -
Nêu Câu Hỏi: Làm thế nào để nhớ công thức thể tích hình cầu một cách dễ dàng?
Trả Lời Chi tiết Câu Hỏi: Bạn có thể liên tưởng đến hình ảnh một quả cam được chia thành 4 phần, với mỗi phần có thể tích xấp xỉ πr³. -
Nêu Câu Hỏi: Nguyên lý Cavalieri có áp dụng được cho các hình dạng khác không?
Trả Lời Chi tiết Câu Hỏi: Có, Nguyên lý Cavalieri có thể áp dụng cho nhiều hình dạng khác nhau để so sánh thể tích. -
Nêu Câu Hỏi: Tích phân có vai trò gì trong việc tính thể tích các hình không gian?
Trả Lời Chi tiết Câu Hỏi: Tích phân là một công cụ mạnh mẽ để tính thể tích các hình không gian phức tạp.