Chứng Minh Công Thức Tính Diện Tích Hình Thang là một kiến thức toán học cơ bản, quan trọng và được áp dụng rộng rãi trong thực tế. Bài viết này sẽ hướng dẫn bạn chứng minh công thức này một cách chi tiết, dễ hiểu và cung cấp thêm những kiến thức bổ ích liên quan.
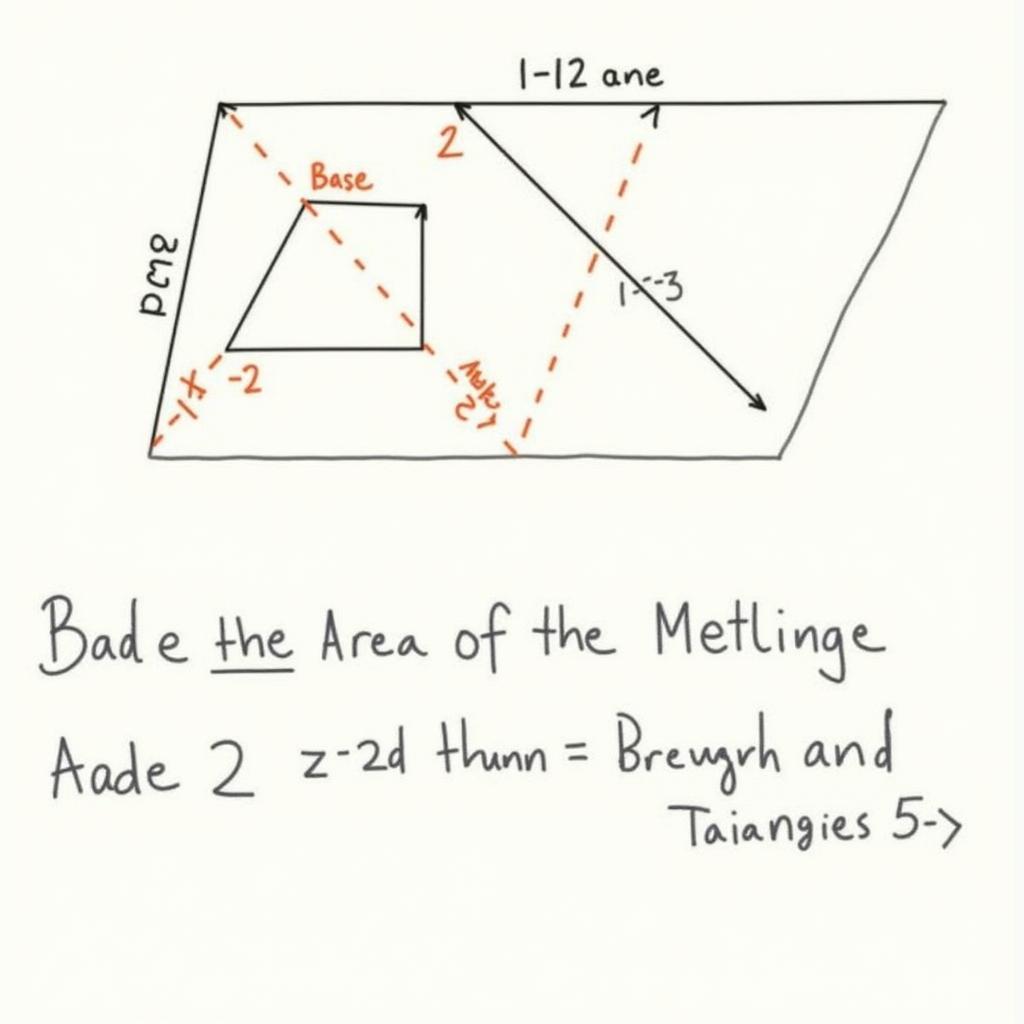Chứng minh công thức diện tích hình thang
Hình Thang Là Gì? Và Các Yếu Tố Cấu Thành
Hình thang là một tứ giác có hai cạnh đối song song, được gọi là hai đáy. Khoảng cách vuông góc giữa hai đáy này được gọi là chiều cao của hình thang. Hai cạnh còn lại không song song được gọi là hai cạnh bên. Hiểu rõ các yếu tố này là bước đầu tiên để chứng minh công thức tính diện tích hình thang. Có những loại hình thang đặc biệt như hình thang cân (hai cạnh bên bằng nhau), hình thang vuông (một góc vuông).
Chứng Minh Công Thức Diện Tích Hình Thang Bằng Cách Chia Hình
Một cách phổ biến để chứng minh công thức tính diện tích hình thang là chia hình thang thành hai tam giác bằng cách vẽ một đường chéo.
- Bước 1: Vẽ đường chéo chia hình thang thành hai tam giác.
- Bước 2: Xác định đáy và chiều cao của mỗi tam giác. Đáy của mỗi tam giác chính là một đáy của hình thang, và chiều cao của cả hai tam giác bằng chiều cao của hình thang.
- Bước 3: Tính diện tích mỗi tam giác theo công thức: Diện tích tam giác = (1/2) x đáy x chiều cao.
- Bước 4: Cộng diện tích hai tam giác lại. Ta được: Diện tích hình thang = (1/2) x đáy lớn x chiều cao + (1/2) x đáy nhỏ x chiều cao = (1/2) x (đáy lớn + đáy nhỏ) x chiều cao.
Phương Pháp Chứng Minh Khác: Ghép Hình Thành Hình Bình Hành
Một cách chứng minh khác là ghép hai hình thang giống nhau thành một hình bình hành. Diện tích hình bình hành gấp đôi diện tích hình thang và bằng tích của một cạnh đáy và chiều cao. Từ đó, ta suy ra công thức tính diện tích hình thang.
What chứng minh công thức tính diện tích hình thang?
Chứng minh công thức tính diện tích hình thang là việc sử dụng các phương pháp toán học để khẳng định tính đúng đắn của công thức: Diện tích = (1/2) x (đáy lớn + đáy nhỏ) x chiều cao.
Who chứng minh công thức tính diện tích hình thang?
Các nhà toán học đã chứng minh công thức này từ xa xưa. Học sinh cũng được học cách chứng minh công thức này trong chương trình toán học.
When chứng minh công thức tính diện tích hình thang?
Công thức này được chứng minh và sử dụng từ rất lâu trong lịch sử toán học. Học sinh thường được học chứng minh công thức này ở bậc trung học cơ sở.
Where chứng minh công thức tính diện tích hình thang?
Việc chứng minh công thức này được thực hiện trong các tài liệu toán học, sách giáo khoa, và trên các nền tảng học tập trực tuyến.
Why chứng minh công thức tính diện tích hình thang?
Chứng minh công thức giúp chúng ta hiểu rõ bản chất và nguồn gốc của công thức, từ đó áp dụng một cách chính xác và linh hoạt trong giải toán và thực tiễn. Việc chứng minh công thức tính diện tích hình thang có ứng dụng trong nhiều lĩnh vực, từ xây dựng, kiến trúc đến thiết kế và đo đạc. chứng khoán thành công tuyển dụng
How chứng minh công thức tính diện tích hình thang?
Có nhiều cách chứng minh, phổ biến nhất là chia hình thang thành hai tam giác hoặc ghép hai hình thang thành hình bình hành. tuyển công chứng viên tại hà nội
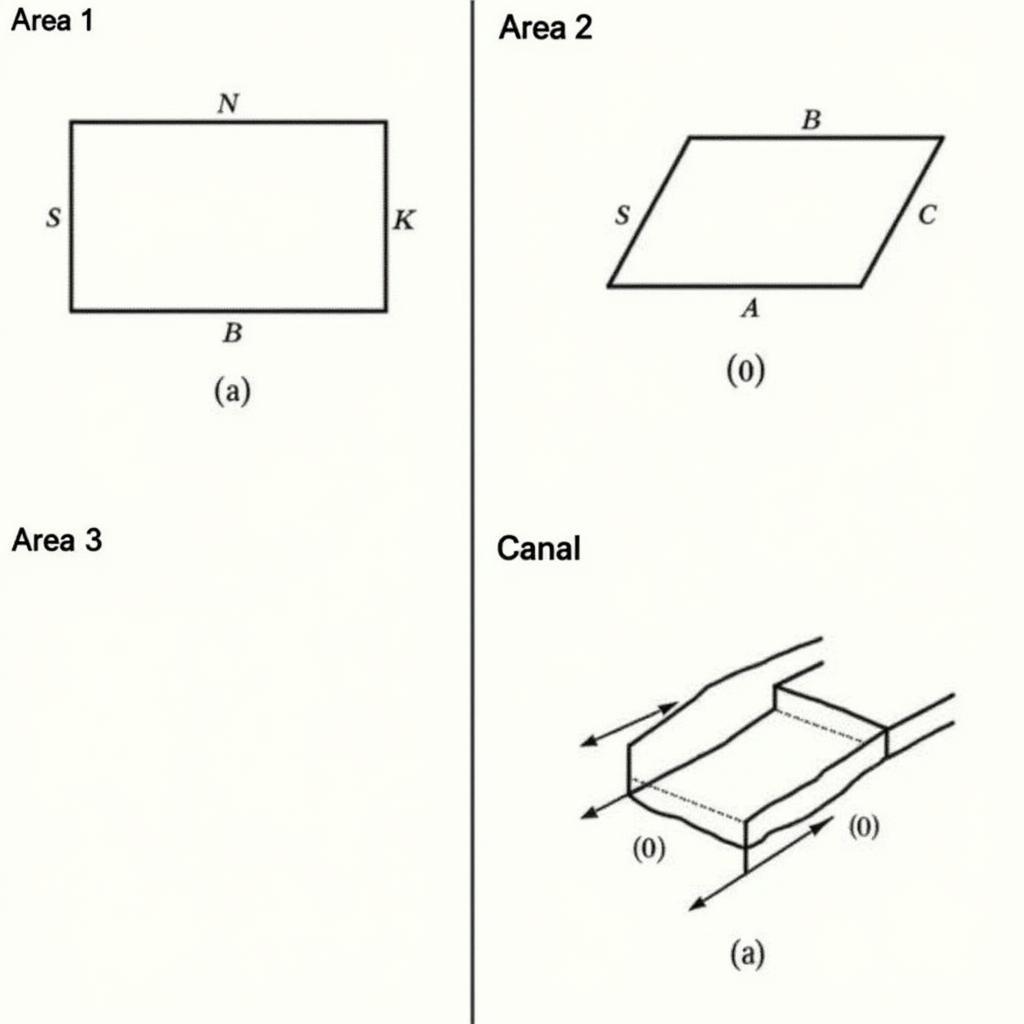Áp dụng công thức diện tích hình thang
Bảng Giá Chi tiết (Ví dụ minh họa)
| Loại hình thang | Đáy lớn (m) | Đáy nhỏ (m) | Chiều cao (m) | Diện tích (m²) |
|---|---|---|---|---|
| Hình thang vuông | 5 | 3 | 4 | 16 |
| Hình thang cân | 6 | 2 | 3 | 12 |
Ông Nguyễn Văn A, chuyên gia toán học tại Đại học X, chia sẻ: “Việc chứng minh công thức tính diện tích hình thang không chỉ là một bài tập toán học đơn thuần, mà còn giúp rèn luyện tư duy logic và khả năng phân tích hình học.”
Bà Trần Thị B, giáo viên toán THCS Y, cho biết: “Học sinh cần nắm vững cách chứng minh công thức này để áp dụng vào giải các bài toán thực tế, ví dụ như tính diện tích mảnh đất hình thang.”
Kết luận lại, chứng minh công thức tính diện tích hình thang là một kiến thức cơ bản và quan trọng. Hy vọng bài viết này đã giúp bạn hiểu rõ cách chứng minh và áp dụng công thức này. chứng minh công thức thể tích hình nêm Hãy luyện tập thêm để thành thạo hơn. chứng minh công thức chiều cao một nửa đỉnh các công thức chứng minh tứ giác nội tiếp
FAQ
-
Nêu Câu Hỏi: Công thức tính diện tích hình thang là gì?
Trả Lời Chi tiết Câu Hỏi: Diện tích = (1/2) x (đáy lớn + đáy nhỏ) x chiều cao. -
Nêu Câu Hỏi: Làm thế nào để phân biệt hình thang cân và hình thang vuông?
Trả Lời Chi tiết Câu Hỏi: Hình thang cân có hai cạnh bên bằng nhau, hình thang vuông có một góc vuông. -
Nêu Câu Hỏi: Chiều cao của hình thang là gì?
Trả Lời Chi tiết Câu Hỏi: Chiều cao là khoảng cách vuông góc giữa hai đáy của hình thang. -
Nêu Câu Hỏi: Có những cách nào để chứng minh công thức tính diện tích hình thang?
Trả Lời Chi tiết Câu Hỏi: Có thể chia hình thang thành hai tam giác hoặc ghép hai hình thang thành hình bình hành. -
Nêu Câu Hỏi: Ứng dụng của công thức tính diện tích hình thang trong thực tế là gì?
Trả Lời Chi tiết Câu Hỏi: Ứng dụng trong đo đạc đất đai, xây dựng, kiến trúc… -
Nêu Câu Hỏi: Hình thang có bao nhiêu đáy?
Trả Lời Chi tiết Câu Hỏi: Hình thang có hai đáy là hai cạnh đối song song. -
Nêu Câu Hỏi: Diện tích hình thang có thể âm được không?
Trả Lời Chi tiết Câu Hỏi: Không, diện tích hình thang luôn là một số dương. -
Nêu Câu Hỏi: Nếu biết diện tích, đáy lớn và chiều cao, làm thế nào để tính đáy nhỏ?
Trả Lời Chi tiết Câu Hỏi: Đáy nhỏ = (2 x Diện tích / Chiều cao) – Đáy lớn. -
Nêu Câu Hỏi: Có công thức nào khác để tính diện tích hình thang không?
Trả Lời Chi tiết Câu Hỏi: Không, công thức trên là công thức duy nhất để tính diện tích hình thang. -
Nêu Câu Hỏi: Tại sao cần phải học chứng minh công thức tính diện tích hình thang?
Trả Lời Chi tiết Câu Hỏi: Học chứng minh giúp hiểu sâu hơn về công thức và rèn luyện tư duy logic.