Chứng minh công thức thể tích hình cầu là một vấn đề toán học thú vị và có tính ứng dụng cao. Bài viết này sẽ hướng dẫn bạn chi tiết cách chứng minh công thức này, từ cơ bản đến nâng cao, cùng với những ví dụ minh họa dễ hiểu.

Khám Phá Công Thức Thể Tích Hình Cầu

Công thức tính thể tích hình cầu là V = (4/3)πr³, với r là bán kính hình cầu. Nhưng bạn đã bao giờ tự hỏi tại sao lại là (4/3)πr³ chưa? Chúng ta sẽ cùng nhau tìm hiểu điều đó. 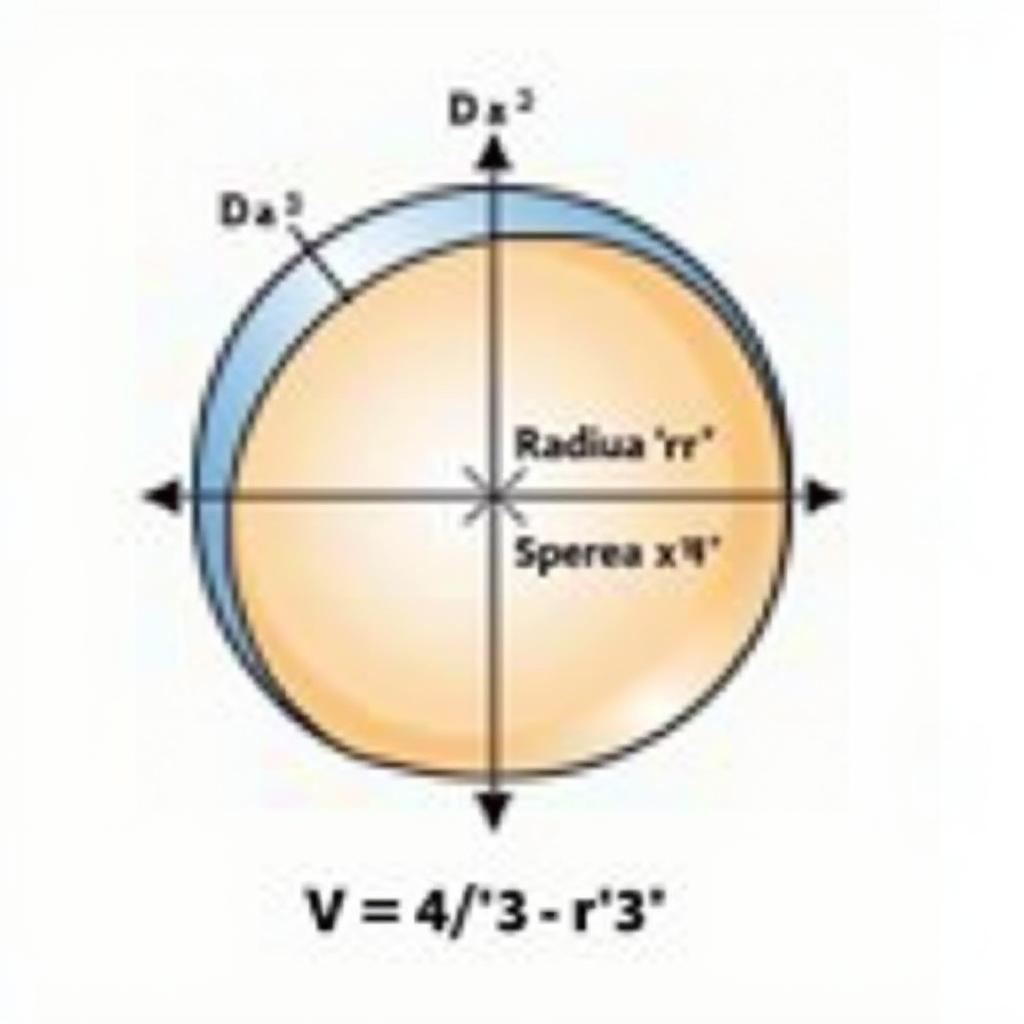Chứng minh công thức thể tích hình cầu Một trong những cách tiếp cận phổ biến nhất là sử dụng tích phân. Tuy nhiên, trước khi đi vào chi tiết, chúng ta cần nắm vững một số khái niệm cơ bản.

Nguyên Lý Cavalieri và Ứng Dụng trong Chứng Minh

Nguyên lý Cavalieri là chìa khóa để chứng minh công thức thể tích hình cầu. Nguyên lý này nói rằng nếu hai hình có cùng chiều cao và mỗi mặt cắt song song với mặt đáy và cách mặt đáy một khoảng bằng nhau có diện tích bằng nhau, thì hai hình đó có cùng thể tích. Chúng ta sẽ sử dụng nguyên lý này để so sánh thể tích hình cầu với thể tích của một hình khác mà ta đã biết công thức tính thể tích. 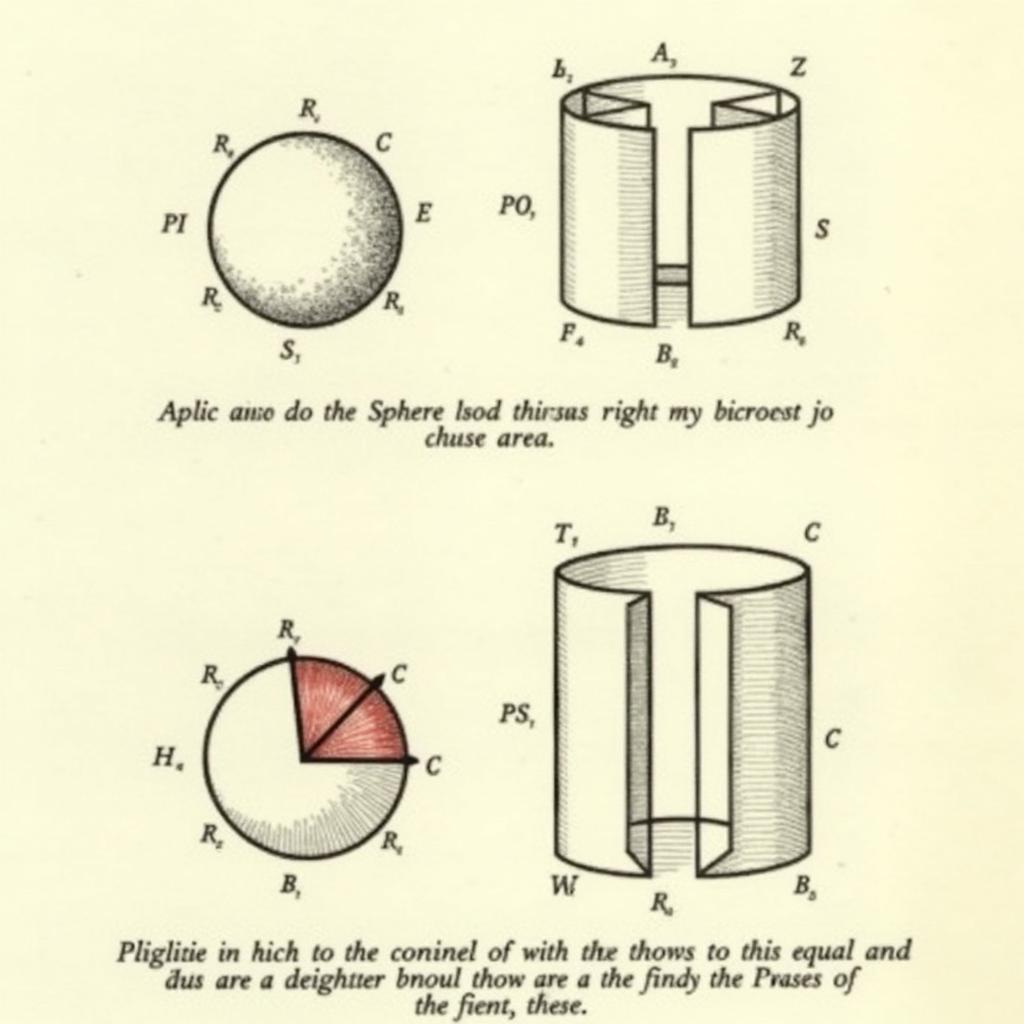Nguyên lý Cavalieri và hình cầu

So Sánh Hình Cầu với Hình Trụ và Hình Nón

Để áp dụng nguyên lý Cavalieri, ta sẽ xem xét một hình trụ có bán kính đáy là r và chiều cao là 2r, sau đó loại bỏ hai hình nón đối xứng nhau ở hai đầu hình trụ, mỗi hình nón có bán kính đáy và chiều cao đều bằng r. Thể tích phần còn lại của hình trụ sẽ được chứng minh là bằng thể tích hình cầu.

Chứng Minh Công Thức Bằng Tích Phân

Phần này sẽ trình bày chi tiết cách chứng minh công thức thể tích hình cầu bằng tích phân. Ta sẽ sử dụng tích phân đĩa để tính thể tích hình cầu. công ty chứng khoán tuyển dụng tại hà nội Quá trình tích phân sẽ liên quan đến việc chia hình cầu thành vô số đĩa mỏng và tính tổng thể tích của các đĩa này.

Tích Phân Đĩa và Thể Tích Hình Cầu

Bằng cách sử dụng tích phân đĩa, ta có thể tính thể tích hình cầu bằng cách tích phân diện tích của các mặt cắt hình tròn theo chiều cao của hình cầu.

What chứng minh công thức the tích hình cầu?

Chứng minh công thức thể tích hình cầu là việc sử dụng các phương pháp toán học như tích phân hoặc nguyên lý Cavalieri để khẳng định công thức V = (4/3)πr³ là chính xác.

Who chứng minh công thức the tích hình cầu?

Mặc dù không có một cá nhân cụ thể được công nhận là người đầu tiên chứng minh công thức này, nhưng Archimedes được ghi nhận là người đã có những đóng góp quan trọng trong việc tìm ra thể tích hình cầu. v phạm trong hoạt động công chứng

When chứng minh công thức the tích hình cầu?

Việc chứng minh công thức thể tích hình cầu đã được thực hiện từ thời cổ đại, với những đóng góp đáng kể từ thời Archimedes.

Where chứng minh công thức the tích hình cầu?

Công thức thể tích hình cầu được chứng minh và ứng dụng rộng rãi trong toán học, vật lý và nhiều lĩnh vực khác. cơ cấu sở hữu công ty chứng khoán rồng việt

Why chứng minh công thức the tích hình cầu?

Việc chứng minh công thức này là cần thiết để đảm bảo tính chính xác của nó và giúp chúng ta hiểu sâu hơn về hình học không gian.

How chứng minh công thức the tích hình cầu?

Có nhiều cách để chứng minh, bao gồm sử dụng tích phân, nguyên lý Cavalieri, hoặc các phương pháp hình học khác. các công ty thủy điện trên sàn chứng khoán Các phương pháp chứng minh công thức thể tích hình cầu

Theo chuyên gia toán học Nguyễn Văn A, “Việc hiểu rõ nguyên lý Cavalieri là chìa khóa để nắm bắt được bản chất của chứng minh công thức thể tích hình cầu.”

Bà Trần Thị B, một nhà giáo dục giàu kinh nghiệm, chia sẻ: “Việc chứng minh công thức thể tích hình cầu không chỉ là một bài tập toán học mà còn giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề.”

Kết luận lại, chứng minh công thức thể tích hình cầu là một phần quan trọng của toán học. Bài viết này đã cung cấp cho bạn một cái nhìn tổng quan về các phương pháp chứng minh và hy vọng sẽ giúp bạn hiểu rõ hơn về công thức này. Hãy tiếp tục khám phá và tìm hiểu thêm về những điều thú vị trong thế giới toán học! phần mềm công chứng uchi

FAQ

1. Nêu Câu Hỏi: Công thức thể tích hình cầu là gì?
   Trả Lời Chi tiết Câu Hỏi: Công thức thể tích hình cầu là V = (4/3)πr³, trong đó r là bán kính của hình cầu.

2. Nêu Câu Hỏi: Nguyên lý Cavalieri là gì?
   Trả Lời Chi tiết Câu Hỏi: Nguyên lý Cavalieri nói rằng nếu hai hình có cùng chiều cao và mỗi mặt cắt song song với mặt đáy và cách mặt đáy một khoảng bằng nhau có diện tích bằng nhau, thì hai hình đó có cùng thể tích.

3. Nêu Câu Hỏi: Tích phân đĩa là gì?
   Trả Lời Chi tiết Câu Hỏi: Tích phân đĩa là một phương pháp tính thể tích bằng cách tích phân diện tích của các mặt cắt hình tròn theo chiều cao của hình.

4. Nêu Câu Hỏi: Ai là người đầu tiên chứng minh công thức thể tích hình cầu?
   Trả Lời Chi tiết Câu Hỏi: Archimedes được ghi nhận là người đã có những đóng góp quan trọng trong việc tìm ra thể tích hình cầu.

5. Nêu Câu Hỏi: Tại sao cần phải chứng minh công thức thể tích hình cầu?
   Trả Lời Chi tiết Câu Hỏi: Việc chứng minh giúp khẳng định tính chính xác của công thức và giúp hiểu sâu hơn về hình học không gian.

6. Nêu Câu Hỏi: Có những phương pháp nào để chứng minh công thức thể tích hình cầu?
   Trả Lời Chi tiết Câu Hỏi: Có nhiều cách, bao gồm sử dụng tích phân, nguyên lý Cavalieri, hoặc các phương pháp hình học khác.

7. Nêu Câu Hỏi: Làm thế nào để áp dụng công thức thể tích hình cầu trong thực tế?
   Trả Lời Chi tiết Câu Hỏi: Công thức này được sử dụng để tính thể tích của các vật thể hình cầu, ví dụ như quả bóng, bể chứa hình cầu, v.v.

8. Nêu Câu Hỏi: Thể tích hình cầu có liên quan gì đến diện tích bề mặt của nó?
   Trả Lời Chi tiết Câu Hỏi: Thể tích và diện tích bề mặt của hình cầu đều liên quan đến bán kính của nó.

9. Nêu Câu Hỏi: Làm thế nào để tính bán kính của hình cầu khi biết thể tích?
   Trả Lời Chi tiết Câu Hỏi: Có thể rút ra công thức tính bán kính từ công thức thể tích: r =∛(3V/4π).

10. Nêu Câu Hỏi: Có tài liệu nào để tìm hiểu thêm về chứng minh công thức thể tích hình cầu?
    Trả Lời Chi tiết Câu Hỏi: Có rất nhiều sách giáo khoa toán học và tài liệu trực tuyến cung cấp thông tin chi tiết về chứng minh này.