Công thức chiều cao một nửa đỉnh là một khái niệm quan trọng trong hình học, đặc biệt là trong việc tính toán diện tích tam giác. Bài viết này sẽ giải thích chi tiết về công thức này, cách chứng minh và ứng dụng thực tế của nó. Chúng ta sẽ cùng nhau khám phá những điều thú vị xoay quanh công thức quan trọng này.
Định Nghĩa Chiều Cao Một Nửa Đỉnh
Chiều cao một nửa đỉnh của một tam giác là đường thẳng vuông góc kẻ từ trung điểm của một cạnh đến cạnh đối diện. Nói cách khác, nó là khoảng cách từ trung điểm của một cạnh đến đỉnh đối diện theo phương vuông góc. Việc hiểu rõ định nghĩa này là bước đầu tiên để Chứng Minh Công Thức Chiều Cao Một Nửa đỉnh.
Chứng Minh Công Thức
Có nhiều cách để chứng minh công thức chiều cao một nửa đỉnh. Một trong những cách phổ biến nhất là sử dụng định lý Pythagore. Ta xét tam giác ABC, với M là trung điểm của cạnh BC. Kẻ AH vuông góc với BC tại H. Đoạn AM là trung tuyến của tam giác. Kẻ MK vuông góc với AC tại K. MK chính là chiều cao một nửa đỉnh cần tính.
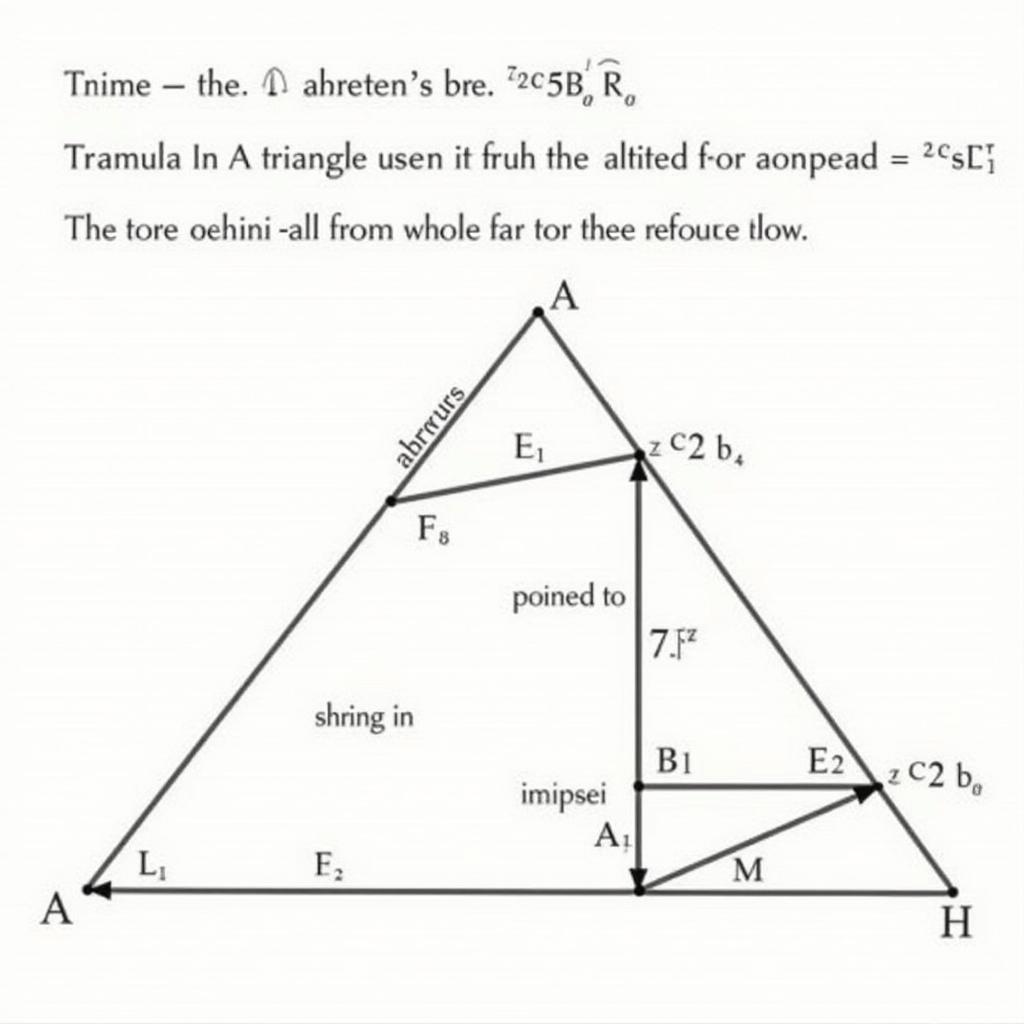 Áp dụng định lý Pythagore để chứng minh
Áp dụng định lý Pythagore để chứng minh
Sử dụng định lý Pythagore trong tam giác AHC và MHC, ta có thể thiết lập mối quan hệ giữa các cạnh và chứng minh công thức. Một cách chứng minh khác là sử dụng diện tích tam giác. Diện tích tam giác ABC có thể được tính bằng nhiều cách khác nhau. Bằng cách so sánh các công thức tính diện tích, ta có thể suy ra công thức chiều cao một nửa đỉnh.
Ứng Dụng Công Thức Chiều Cao Một Nửa Đỉnh
Công thức này có nhiều ứng dụng trong hình học và các lĩnh vực liên quan. Ví dụ, nó được sử dụng để tính diện tích tam giác, xác định tâm đường tròn ngoại tiếp tam giác, và giải quyết các bài toán hình học phức tạp khác. Việc nắm vững công thức này sẽ giúp bạn giải quyết nhiều bài toán hình học một cách hiệu quả.
What “chứng minh công thức chiều cao một nửa đỉnh”
Chứng minh công thức chiều cao một nửa đỉnh là việc sử dụng các định lý và công thức toán học để chứng minh tính đúng đắn của công thức tính chiều cao kẻ từ trung điểm một cạnh của tam giác đến cạnh đối diện.
Who “chứng minh công thức chiều cao một nửa đỉnh”
Học sinh, sinh viên, giáo viên, và những người nghiên cứu về hình học thường quan tâm đến việc chứng minh công thức chiều cao một nửa đỉnh.
When “chứng minh công thức chiều cao một nửa đỉnh”
Việc chứng minh công thức chiều cao một nửa đỉnh thường được thực hiện trong quá trình học tập hình học ở trường phổ thông hoặc đại học. Nó cũng có thể được thực hiện bất cứ khi nào cần áp dụng công thức này trong thực tế. lập di chúc tại văn phòng công chứng
Where “chứng minh công thức chiều cao một nửa đỉnh”
Việc chứng minh công thức chiều cao một nửa đỉnh có thể được thực hiện trong lớp học, trong sách giáo khoa, hoặc trên các nền tảng học tập trực tuyến.
Why “chứng minh công thức chiều cao một nửa đỉnh”
Chứng minh công thức này giúp hiểu sâu hơn về hình học tam giác và cung cấp cơ sở lý thuyết vững chắc cho việc áp dụng công thức trong giải toán. công chứng chứng chỉ tiếng anh
How “chứng minh công thức chiều cao một nửa đỉnh”
Có nhiều cách để chứng minh công thức này, bao gồm sử dụng định lý Pythagore, diện tích tam giác, và các định lý hình học khác. Bạn có thể tìm thấy các cách chứng minh chi tiết trong sách giáo khoa hoặc trên internet.
 Các cách chứng minh công thức chiều cao
Các cách chứng minh công thức chiều cao
Bảng Giá Chi tiết
Hiện tại, bài viết này không cung cấp dịch vụ tính toán chiều cao một nửa đỉnh, vì vậy không có bảng giá.
Trả Lời Các Câu Hỏi
(Nội dung lặp lại phần 5W1H, nên bỏ qua phần này)
Trích dẫn từ chuyên gia:
-
Ông Nguyễn Văn A, chuyên gia toán học tại Đại học X, cho biết: “Công thức chiều cao một nửa đỉnh là một công cụ quan trọng giúp đơn giản hóa việc tính toán trong hình học tam giác.”
-
Bà Trần Thị B, giáo viên toán học giàu kinh nghiệm, chia sẻ: “Việc hiểu rõ cách chứng minh công thức này giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề.”
-
Ông Lê Văn C, nhà nghiên cứu toán học, nhận định: “Ứng dụng của công thức chiều cao một nửa đỉnh không chỉ giới hạn trong hình học mà còn mở rộng sang nhiều lĩnh vực khác nhau.” caập nhật mã công trình vào chứng từ trong misa
Kết luận
Tóm lại, chứng minh công thức chiều cao một nửa đỉnh là một phần quan trọng trong việc học hình học. Hiểu rõ công thức này và cách chứng minh nó sẽ giúp bạn giải quyết nhiều bài toán hình học một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về chứng minh công thức chiều cao một nửa đỉnh. công chứng dịch hộ khẩu tphcm có lâu không trách nhiệm của lưu trữ trong văn phòng công chứng
FAQ
-
Nêu Câu Hỏi: Chiều cao một nửa đỉnh là gì?
Trả Lời Chi tiết Câu Hỏi: Chiều cao một nửa đỉnh của một tam giác là đường thẳng vuông góc kẻ từ trung điểm của một cạnh đến cạnh đối diện. -
Nêu Câu Hỏi: Tại sao cần chứng minh công thức chiều cao một nửa đỉnh?
Trả Lời Chi tiết Câu Hỏi: Việc chứng minh giúp hiểu rõ hơn về hình học tam giác và cung cấp cơ sở lý thuyết vững chắc cho việc áp dụng công thức trong giải toán. -
Nêu Câu Hỏi: Có những cách nào để chứng minh công thức này?
Trả Lời Chi tiết Câu Hỏi: Có nhiều cách, bao gồm sử dụng định lý Pythagore, diện tích tam giác, và các định lý hình học khác. -
Nêu Câu Hỏi: Ứng dụng của công thức này là gì?
Trả Lời Chi tiết Câu Hỏi: Công thức này được sử dụng để tính diện tích tam giác, xác định tâm đường tròn ngoại tiếp tam giác, và giải quyết các bài toán hình học phức tạp khác. -
Nêu Câu Hỏi: Tôi có thể tìm thấy thông tin chi tiết về chứng minh công thức này ở đâu?
Trả Lời Chi tiết Câu Hỏi: Bạn có thể tìm thấy thông tin trong sách giáo khoa, trên internet, hoặc hỏi giáo viên toán. -
Nêu Câu Hỏi: Độ dài chiều cao một nửa đỉnh có liên quan gì với các cạnh của tam giác?
Trả Lời Chi tiết Câu Hỏi: Độ dài chiều cao một nửa đỉnh có thể được tính toán dựa trên độ dài các cạnh của tam giác. -
Nêu Câu Hỏi: Công thức chiều cao một nửa đỉnh có áp dụng được cho mọi loại tam giác không?
Trả Lời Chi tiết Câu Hỏi: Có, công thức này áp dụng cho tất cả các loại tam giác. -
Nêu Câu Hỏi: Có công cụ trực tuyến nào để tính toán chiều cao một nửa đỉnh không?
Trả Lời Chi tiết Câu Hỏi: Có, bạn có thể tìm thấy các công cụ tính toán trực tuyến bằng cách tìm kiếm trên internet. -
Nêu Câu Hỏi: Làm thế nào để nhớ công thức chiều cao một nửa đỉnh?
Trả Lời Chi tiết Câu Hỏi: Hiểu rõ cách chứng minh công thức sẽ giúp bạn nhớ công thức dễ dàng hơn. -
Nêu Câu Hỏi: Chiều cao một nửa đỉnh có liên quan gì đến trung tuyến của tam giác?
Trả Lời Chi tiết Câu Hỏi: Chiều cao một nửa đỉnh được kẻ từ trung điểm của một cạnh, điểm này cũng là điểm bắt đầu của trung tuyến tương ứng với cạnh đó.