Công thức a1 = 2.r1 và a2 = 2.r2 thường được sử dụng trong hình học, đặc biệt là khi làm việc với các đường tròn và tiếp tuyến. Bài viết này sẽ đi sâu vào việc chứng minh tính đúng đắn của hai công thức này, đồng thời giải thích ý nghĩa và ứng dụng của chúng trong thực tế.

Hiểu Về Công Thức a1 = 2.r1 và a2 = 2.r2

Công thức a1 = 2.r1 và a2 = 2.r2 thể hiện mối quan hệ giữa độ dài cạnh của một hình vuông nội tiếp đường tròn (a1, a2) và bán kính của đường tròn đó (r1, r2). Nói một cách đơn giản, nếu bạn biết bán kính của một đường tròn, bạn có thể dễ dàng tính toán độ dài cạnh của hình vuông nằm gọn trong đường tròn đó và ngược lại.

Chứng Minh Công Thức a1 = 2.r1

Xét một hình vuông nội tiếp đường tròn có bán kính r1. Đường chéo của hình vuông này chính là đường kính của đường tròn. Gọi độ dài cạnh hình vuông là a1. Theo định lý Pythagore, bình phương đường chéo của hình vuông bằng tổng bình phương hai cạnh của nó, tức là (2.r1)^2 = a1^2 + a1^2. Từ đó suy ra 4.r1^2 = 2.a1^2 => a1^2 = 2.r1^2 => a1 = √2.r1. Tuy nhiên, nếu hình vuông ngoại tiếp đường tròn thì đường kính đường tròn bằng cạnh hình vuông, do đó a1 = 2.r1.

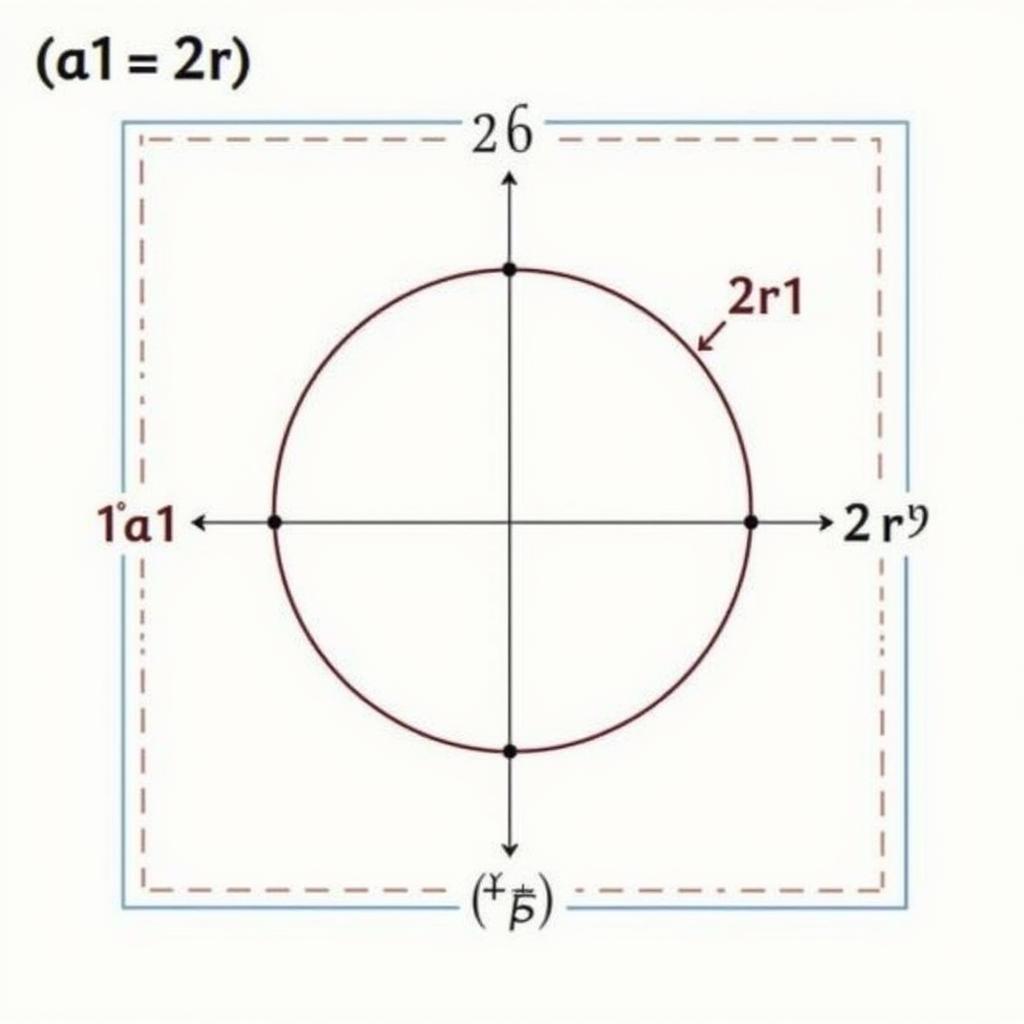Chứng minh công thức a1 = 2r1

Chứng Minh Công Thức a2 = 2.r2

Tương tự, với hình vuông ngoại tiếp đường tròn có bán kính r2 và cạnh a2. Đường kính của đường tròn bằng cạnh của hình vuông. Do đó, a2 = 2.r2.

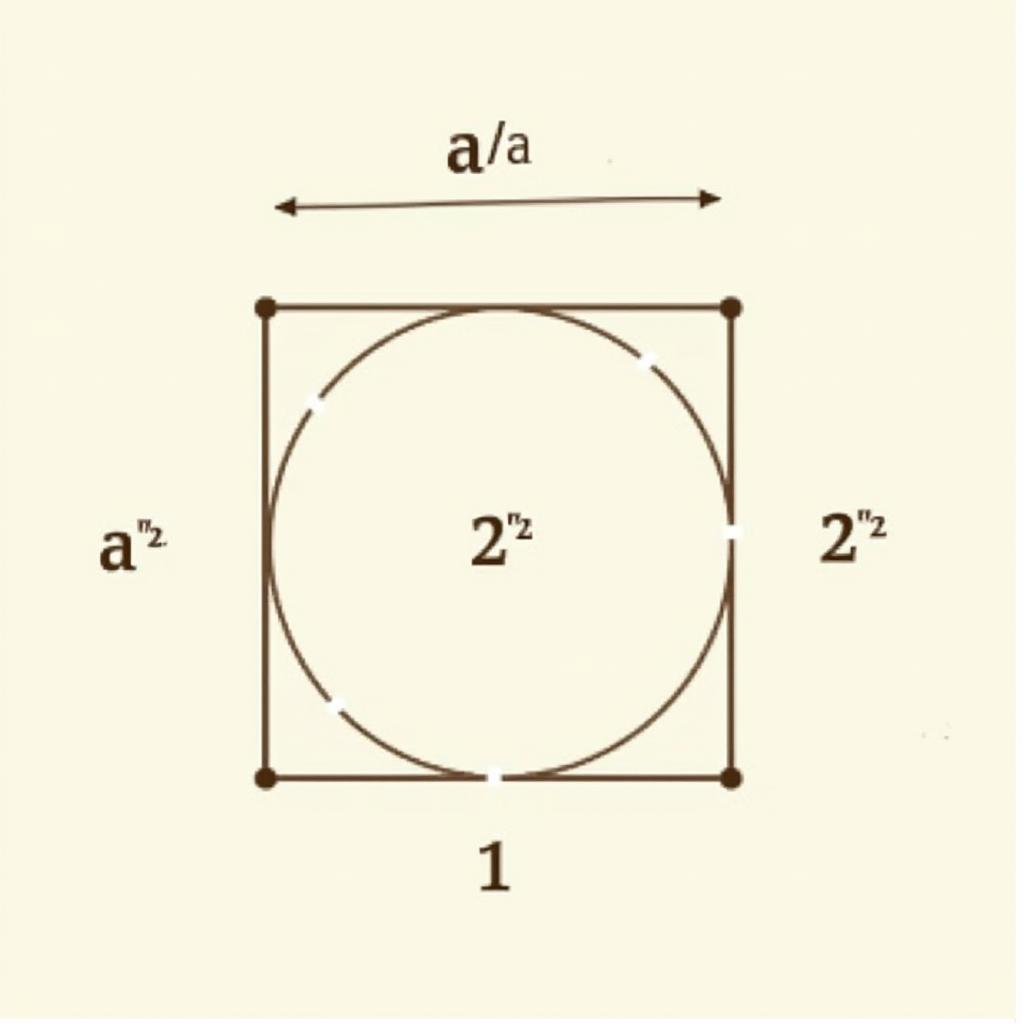Chứng minh công thức a2 = 2r2

Ứng Dụng Của Công Thức a1 = 2.r1 và a2 = 2.r2

Công thức này có nhiều ứng dụng trong thực tế, ví dụ như trong thiết kế, xây dựng, và kỹ thuật. Việc hiểu rõ mối quan hệ giữa hình vuông và đường tròn giúp chúng ta tính toán chính xác kích thước và diện tích của các vật thể.

Trả Lời Các Câu Hỏi:

• What chứng minh công thức a1 = 2.r1 a2 = 2.r2? Bài viết này chứng minh công thức bằng cách sử dụng định lý Pythagore và mối quan hệ giữa đường kính đường tròn và cạnh hình vuông.
• Who sử dụng công thức a1 = 2.r1 a2 = 2.r2? Các kỹ sư, kiến trúc sư, nhà thiết kế và những người làm việc trong lĩnh vực liên quan đến hình học thường sử dụng công thức này.
• When sử dụng công thức a1 = 2.r1 a2 = 2.r2? Khi cần tính toán mối quan hệ giữa hình vuông và đường tròn nội tiếp hoặc ngoại tiếp nó.
• Where áp dụng công thức a1 = 2.r1 a2 = 2.r2? Công thức này được áp dụng trong nhiều lĩnh vực, từ thiết kế, xây dựng đến kỹ thuật.
• Why cần chứng minh công thức a1 = 2.r1 a2 = 2.r2? Việc chứng minh giúp hiểu rõ bản chất của công thức và áp dụng chính xác trong thực tế.
• How chứng minh công thức a1 = 2.r1 a2 = 2.r2? Sử dụng định lý Pythagore và mối quan hệ giữa hình vuông và đường tròn.

Trích dẫn từ Chuyên gia

“Hiểu rõ công thức a1 = 2.r1 và a2 = 2.r2 là nền tảng cho việc giải quyết nhiều bài toán hình học phức tạp hơn,” – Ông Nguyễn Văn A, Chuyên gia Toán học.

“Ứng dụng của công thức này rất rộng rãi, từ việc tính toán diện tích đến thiết kế các công trình xây dựng,” – Bà Trần Thị B, Kỹ sư Xây dựng.

Kết luận

Tóm lại, công thức a1 = 2.r1 và a2 = 2.r2 là một công cụ hữu ích trong hình học. Việc hiểu và áp dụng đúng công thức chứng minh công thức a1 = 2.r1 a2 = 2.r2 sẽ giúp chúng ta giải quyết nhiều vấn đề thực tiễn một cách hiệu quả.

FAQ

• Câu hỏi: Công thức a1 = 2.r1 áp dụng cho trường hợp nào?

  • Trả lời: Áp dụng khi hình vuông ngoại tiếp đường tròn.

• Câu hỏi: Công thức a2 = 2.r2 áp dụng cho trường hợp nào?

  • Trả lời: Áp dụng khi hình vuông ngoại tiếp đường tròn.

• Câu hỏi: Định lý Pythagore được sử dụng như thế nào trong chứng minh?

  • Trả lời: Định lý Pythagore được dùng để thiết lập mối quan hệ giữa cạnh và đường chéo của hình vuông.

• Câu hỏi: Làm thế nào để nhớ công thức này dễ hơn?

  • Trả lời: Liên tưởng đến hình ảnh hình vuông và đường tròn, nhớ rằng cạnh hình vuông bằng đường kính đường tròn khi hình vuông ngoại tiếp đường tròn.

• Câu hỏi: Có tài liệu nào khác để tìm hiểu thêm về công thức này không?

  • Trả lời: Có rất nhiều sách giáo khoa và tài liệu trực tuyến về hình học đề cập đến chủ đề này.